Random Realization of Polyhedral Graphs as Deltahedra

Abstract:

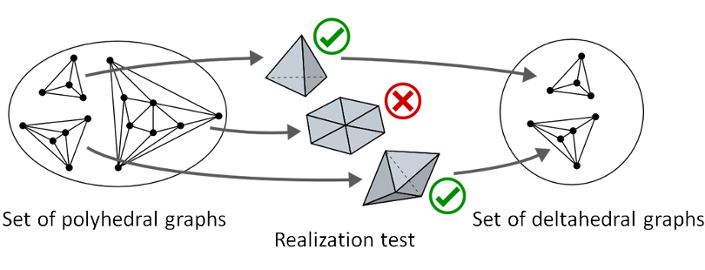
In this paper, we propose a method for realizing a polyhedral graph as a deltahedron, i.e., a polyhedron with congruent equilateral triangles as faces. Our experimental result shows that there are graphs that are not realizable as deltahedra. We provide an example of non-realizable graphs which are obtained by trying to construct deltahedra from each of the simple cubic polyhedral graphs with up to 10 vertices. We also show that the infinite families of non-realizable graphs can be obtained by solving the graph isomorphism problem.

In Japanese:

The list of reconstructed polyhedra is here.

Sources for reconstruction (graph realization) is available on my github.

As stand-alone software, Deltamod
As Blender addons, planar code importer and triangle regularizaion

Naoya Tsuruta, Jun Mitani, Yoshihiro Kanamori, Yukio Fukui, "Random Realization of Polyhedral Graphs as Deltahedra", Journal of Geometry Graphics, Vol.19, No.2, pp.227-236, 2016. PDF
Naoya Tsuruta, Jun Mitani, Yoshihiro Kanamori and Yukio Fukui, "Enumeration of Deltahedral Graphs with up to 10 Vertices", The 16th International Conference on Geometry and Graphics (ICGG2014), Innsbruck, Austria, August 4–8, 2014.
鶴田直也, 三谷純, 金森由博，福井幸男, "面数が16以下の非凸デルタ多面体の数え上げ", 2012年度日本図学会秋季大会, 東京, 学術講演論文集, pp.63-68, 2012/12/15-16.